Scattering by horizontally aligned particles is characterized by four
quantities: ZV (or ZH),
![]() ,
,
![]() ,
and f. Each of the
quantities has an associated propagation effect, namely AV (or AH),
DA = (AH/AV),
,
and f. Each of the
quantities has an associated propagation effect, namely AV (or AH),
DA = (AH/AV), ![]() ,
and
,
and
![]() .
In each case it is the latter
three quantities that affect the polarization state, as in expressions
(10) through (12). The manner in which the different
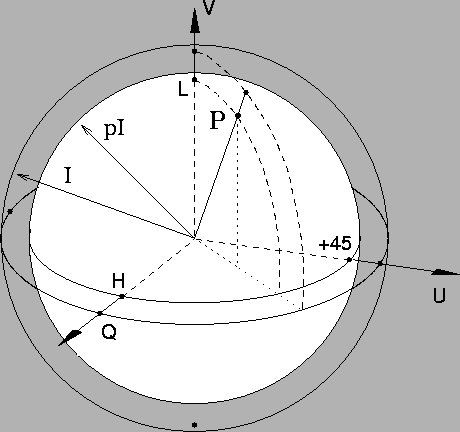
quantities change the polarization state on the Poincaré sphere is shown in
Figure 5. The changes are best described in terms of the
spherical angles
.
In each case it is the latter
three quantities that affect the polarization state, as in expressions
(10) through (12). The manner in which the different
quantities change the polarization state on the Poincaré sphere is shown in
Figure 5. The changes are best described in terms of the
spherical angles ![]() and
and ![]() .
.
![]() is the angle that the
polarization state makes with the +Q or H axis and represents the polar
angle of a spherical coordinate system for which
is the angle that the
polarization state makes with the +Q or H axis and represents the polar
angle of a spherical coordinate system for which ![]() or H is the z-axis.
Positive
or H is the z-axis.
Positive
![]() values cause the polarization state to move toward the
H polarization point by enhancing the H component of the signal relative
to the V component. Positive
values cause the polarization state to move toward the
H polarization point by enhancing the H component of the signal relative
to the V component. Positive
![]() therefore decreases
therefore decreases ![]() .
Differential attenuation (DA) by horizontally oriented particles does the
opposite and causes the polarization state to move toward the Vpolarization point, increasing
.
Differential attenuation (DA) by horizontally oriented particles does the
opposite and causes the polarization state to move toward the Vpolarization point, increasing ![]() .
.
 |
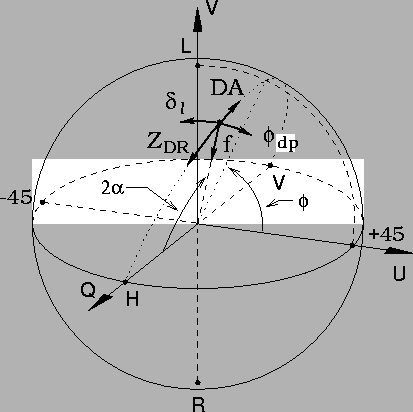 |
The differential phase effects of horizontally aligned particles (![]() and
and
![]() )
change the relative phase of the H and V components but
not their amplitudes. Q therefore remains constant and the polarization
state changes along a circle parallel to the U-V plane. This is called the
)
change the relative phase of the H and V components but
not their amplitudes. Q therefore remains constant and the polarization
state changes along a circle parallel to the U-V plane. This is called the
![]() direction;
direction; ![]() is the azimuthal angle of the spherical coordinate
system. It is also the same as the phase of the cross-covariance W(Equation 1).
is the azimuthal angle of the spherical coordinate
system. It is also the same as the phase of the cross-covariance W(Equation 1). ![]() due to horizontally aligned particles
causes
due to horizontally aligned particles
causes ![]() to decrease (Equation 11). A positive
to decrease (Equation 11). A positive
![]() would cause
would cause ![]() to increase, but
to increase, but
![]() for horizontally oriented
particles is negative and therefore changes the polarization state in the
same direction as
for horizontally oriented
particles is negative and therefore changes the polarization state in the
same direction as ![]() .
.
Finally, changes in the unpolarized component of the radar signal cause
the degree of polarization to change, and thereby changes the radius
of the Poincaré sphere. Aligned particles produce an unpolarized component
when the particles have a variety of shapes. The unpolarized component
can be generated during the backscattering itself or during propagation
by means of forward scattering, and directly affects the correlation
coefficient ![]() (Equation 12).
(Equation 12). ![]() and pare therefore related; the relationship is presented in the appendix.
When the H and V powers are nearly equal,
and pare therefore related; the relationship is presented in the appendix.
When the H and V powers are nearly equal,
![]() ;
exact
equality occurs when the powers are equal. The condition for this being
true is that the polarization state remains in the vicinity of the
;
exact
equality occurs when the powers are equal. The condition for this being
true is that the polarization state remains in the vicinity of the ![]() -
-![]() plane, which will generally be the case if the radar transmits nearly equal
H and V powers and is not depolarized by an unusual amount. (It also
holds both for simultaneous or alternating H and V transmissions.)
plane, which will generally be the case if the radar transmits nearly equal
H and V powers and is not depolarized by an unusual amount. (It also
holds both for simultaneous or alternating H and V transmissions.)
In the vicinity of the ![]() -
-![]() plane, therefore, shape variability changes
the polarization state in the radial direction. The degree of polarization
is reduced by the same amount as
plane, therefore, shape variability changes
the polarization state in the radial direction. The degree of polarization
is reduced by the same amount as ![]() ,
namely by the fractional shape
correlation coefficient f. The different types of changes are therefore
orthogonal or nearly orthogonal to each other in the Poincaré sphere space.
,
namely by the fractional shape
correlation coefficient f. The different types of changes are therefore
orthogonal or nearly orthogonal to each other in the Poincaré sphere space.
Independent of the polarization state, the polarization changes due to
horizontally aligned particles are azimuthally symmetric about the ![]() or
H axis of the Poincaré sphere. In other words, they do not depend on the
particular value of
or
H axis of the Poincaré sphere. In other words, they do not depend on the
particular value of ![]() .
Thus, circular, slant linear, or elliptical
polarizations may be transmitted with the same effect, as long as they
contain the same relative amounts of H and V power. H and Vsignals lie on the axis of symmetry and are therefore do not have their
polarization state changed by horizontally aligned particles. These are
termed the the characteristic polarizations of the particles (Oguchi, 1983).
.
Thus, circular, slant linear, or elliptical
polarizations may be transmitted with the same effect, as long as they
contain the same relative amounts of H and V power. H and Vsignals lie on the axis of symmetry and are therefore do not have their
polarization state changed by horizontally aligned particles. These are
termed the the characteristic polarizations of the particles (Oguchi, 1983).
The above describes the polarization changes qualitatively. The
different effects have been seen in the observations of the previous
section. A quantitative description of the changes is presented by Scott
(1999) and by Krehbiel and Scott (1999). The changes are determined by
transforming from the rationalized covariance variables (WV, WH/WV,
![]() ,
,
![]() )
of Equations (10) through (13)
to the spherical Stokes coordinates (I,
)
of Equations (10) through (13)
to the spherical Stokes coordinates (I, ![]() ,
,
![]() ,
p).
,
p).