Relation between measurements in circular and linear polarization bases.

The alignment direction observations illustrate the relation between linear and circular polarization measurements, as we now discuss. Measurements in a circular polarization basis are characterized by the covariances W₁= W_L, W₂= W_R, and W = W_LR. Rather than work with the rationalized quantities W_L/W_R and $\rho_{{LR}}= W_{LR}/\sqrt{W_LW_R}$, as is convenient in a linear polarization basis, circular polarization measurements are better characterized by the quantity W/W₂, where W₂ is the co-polar return. This is because W/W₂ better reflects the meteorological parameters being measured than the W_L/W_R or $\rho_{{LR}}$ do. The W/W₂ approach was formulated by Barge (1972), Humphries (1974), and McCormick and Hendry (1975), who derived expressions relating W/W₂ to the polarization characteristics of the propagation and scattering medium. The relations have formed the basis for interpreting circular polarization measurements in a number of studies (e.g., McCormick and Hendry, 1975, 1979; Hendry and Antar, 1984; Bringi and Hendry, 1990; Metcalf, 1995, 1997); Krehbiel et al., 1996) but are conceptually and analytically difficult to understand. It has also been difficult to understand how circular and linear observations are related, or how well quantities such as $Z_{\rm DR}$ and $\phi_{dp}$ can be determined from circular polarization measurements (e.g., McCormick, 1979; Torlaschi and Holt, 1993). For this reason many meterological radars have used linear polarization.

The Poincaré sphere approach provides a good way of showing how circular and linear polarization measurements are related. In particular, W/W₂represents a stereographic projection of the polarization state onto a plane tangent to the Poincaré sphere (Scott, 1999). This is illustrated in Figure 9. The plane is tangent at the copolar circular polarization point (considered for simplicity to be LHC) while the projection is from the orthogonal polarization point (RHC). Because W₂ corresponds to the total signal power (polarized plus unpolarized), both the tangent and the projection points are on the surface of the outer, total power sphere, while the polarization state itself is on the inner, Poincaré sphere (see Figure 4).

  

Figure 9: The geometrical relation between W/W₂ measurements and the Poincaré sphere representation of the polarization state.

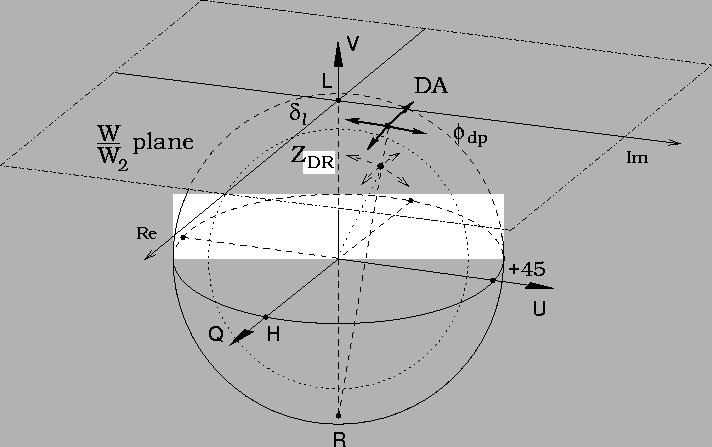The above picture shows why W/W₂ has been a useful quantity in circular polarization measurements; the depolarization effects of horizontally aligned particles produce nearly orthogonal motions in the W/W₂ plane. Also, the depolarization produced by non-horizontally aligned particles is simply rotated from that produced by horizontally aligned particles. From Figure 8, the polarization changes due to particles aligned at an angle $\tau$ are rotated by an angle $2\tau$ in the W/W₂plane. The latter has formed the basis for determining alignment directions using the W/W₂ approach. Differential propagation phase due to horizontally aligned particles causes upward motion of W/W₂, in the positive imaginary direction (Figure 10a), while that due to vertically aligned particles causes downward motion in the negative imaginary direction (Figure 10b). The Poincaré projection plots seen in the data figures of this paper are similar to W/W₂ plots in that they view the Poincaré sphere from above. The trajectories due to horizontally and vertically aligned particles (e.g., Figures 2 and 15) are essentially the same as would be obtained in W/W₂ space, except rotated by $90^\circ$.

  

Figure 10: The polarization trajectory in W/W₂ space a) through horizontally aligned particles in the rain region of a storm (top), and b) through a region of ice crystals aligned vertically by electric forces in the upper part of a storm (bottom). The real and imaginary axes are directed to the right and upward, respectively.

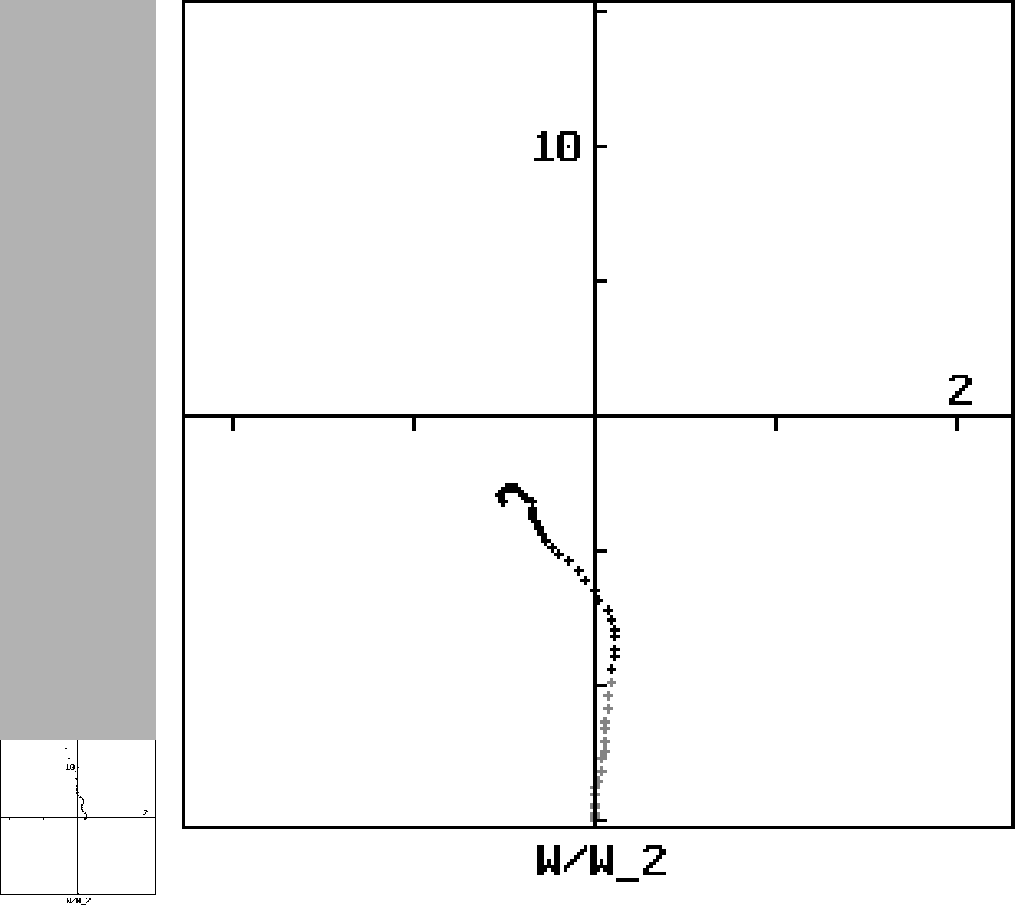The geometrical interpretation highlights two major difficulties with the W/W₂ approach. The first is that the projection is a non-linear function of the polarization state. This complicates the W/W₂ formulations and has limited the extent to which the formulations can be expressed analytically. The second difficulty is that W/W₂ by itself represents the polarization state in terms of only two variables (the real and imaginary parts of W/W₂, for example), while the actual polarization state is specified by three quantities (e.g., ${\rm Q}$, ${{\rm U}}$, ${{\rm V}}$, or $\alpha$, $\phi$, p). If the radar signal remained fully polarized (p = 1), a given polarization state on the surface of the Poincaré sphere would correspond uniquely to a point in W/W₂space and the mapping would be conformal. The radar signal does not remain fully polarized, however, and can develop a significant unpolarized component. When this happens, the resulting changes in the degree of polarization causes the W/W₂ projection point to move radially in and out from the plane's origin, making the mapping non-conformal. (This explains some odd features that have not been understood in W/W₂ trajectories, such as why the trajectories sometimes have `loops'.) The meteorological formulations for W/W₂ have not considered partial polarization and would probably become hopelessly complicated by its inclusion.

The above difficulties are not inherent to the use of circular polarization, only to the W/W₂ approach of representing the measurements. Circular polarization measurements can be well represented in covariance or Poincaré sphere space (Torlaschi and Holt, 1993, 1998; Krehbiel and Scott, 1999).