


Next: Relation of g and
Up: Appendix
Previous: Appendix
The signal covariances W1, W2, and W represent the powers of the
radar signal in orthogonal polarizations and the magnitude and phase of the
cross-covariance or correlated power of the two polarizations. They can be
combined into one entity called the coherency matrix J,
![\begin{displaymath}J = \left[ \begin{array}{cc} W_1 & W \\ W^\ast & W_2 \end{array} \right]
\end{displaymath}](img120.gif) |
(20) |
The coherency matrix can be decomposed into its polarized and unpolarized
components, as
![\begin{displaymath}J =
\left[ \begin{array}{cc} W_1 & W \\ W^\ast & W_2 \end{arr...
... \begin{array}{cc} B & D \\ D^\ast & C \end{array} \right] \ .
\end{displaymath}](img121.gif) |
(21) |
Here, A is the unpolarized power of the signal, which is equal for the
two polarizations, B and C are the polarized powers of the orthogonal
polarization components, and D is cross-power of the polarized component.
Because the components of the unpolarized part of the signal are uncorrelated
with each other (and with the polarized components), D = W. The polarized
matrix has the property that its determinant is zero, namely that
BC
= |D|2.
The covariance measurements determine four quantities: W1, W2, and
|W| and
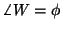 (or, equivalently,
(or, equivalently, ![$\rm Re[W]$](img123.gif) and
and ![$\rm Im[W]$](img124.gif) ).
The decomposed polarization matrices (20) are described by five
quantities (A, B, C, |D|, and
).
The decomposed polarization matrices (20) are described by five
quantities (A, B, C, |D|, and 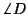 ]), whose values can be obtained
from the covariance measurements and from the polarization constraint
BC
= |D|2. This gives
]), whose values can be obtained
from the covariance measurements and from the polarization constraint
BC
= |D|2. This gives
The decomposed values depend only on the sum and difference of W1 and
W2 and not on W1 or W2 individually.
The above quantities have the interpretation that
(W1 + W2) is the
total signal power, (B + C) is the total polarized power, and 2Ais the total unpolarized power. The degree of polarization p is defined
as the ratio of the polarized power to the total power, namely
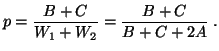 |
|
|
(23) |
From (22), the total polarized power is given by
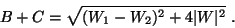 |
(24) |
From this one obtains that
| p |
= |
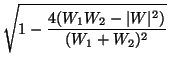 |
(25) |
| |
= |
 |
|
The above formulations apply to any pair of orthogonal polarizations, or
polarization basis. Different polarization bases are related by unitary
transformations; the determinant and trace of J are invariant to such
transformations so that the degree of polarization is independent of
the basis used for the formulations. Similarly, the total polarized and
unpolarized powers are independent of the basis.
Expression (25) can be rewritten in the form
| p |
= |
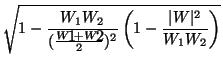 |
|
| |
= |
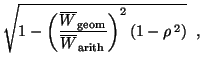 |
(26) |
where
 is the geometric mean
of the orthogonal powers and
is the geometric mean
of the orthogonal powers and
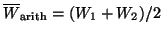 is their arithmetic mean. Rearranging terms gives
is their arithmetic mean. Rearranging terms gives
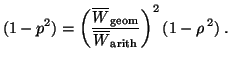 |
|
|
(27) |
The above is a fundamental result that is found in general treatments of
polarization (e.g., Born and Wolf, 1975; Mott, 1986). It relates the degree
of polarization p to the correlation coefficient 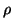 and holds in any
polarization basis.
and holds in any
polarization basis.
From the fact that
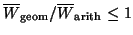 ,
it can be shown that
,
it can be shown that
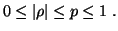 |
|
|
(28) |
Expressed in terms of the polarization ratio W1/W2,
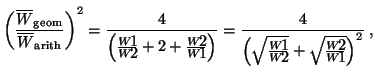 |
|
|
(29) |
When the polarization ratio W2/W1 is unity, the means ratio reaches its
maximum value, also unity. In this case,
| p |
= |
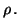 |
(30) |
For non-unity polarization ratios, the means ratio varies as a 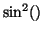 function, going to zero when all the power is contained in W1 or W2.
The degree of polarization is by definition then unity. At intermediate
polarization ratios,
function, going to zero when all the power is contained in W1 or W2.
The degree of polarization is by definition then unity. At intermediate
polarization ratios,
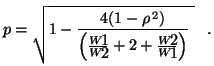 |
|
|
(31) |
In the above expressions, 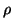 and the means ratio are functions of the
particular basis in which the polarization measurements are made, but p is
independent of basis. In an H-V basis,
and the means ratio are functions of the
particular basis in which the polarization measurements are made, but p is
independent of basis. In an H-V basis,
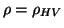 ,
and
,
and
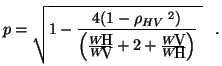 |
|
|
(32) |
A similar relation would hold in a circular polarization basis. Equating
the two would enable the correlation coefficients in the two bases to be
related.



Next: Relation of g and
Up: Appendix
Previous: Appendix
Bill Rison
1999-09-03
![]() (or, equivalently,
(or, equivalently, ![]() and
and ![]() ).
The decomposed polarization matrices (20) are described by five
quantities (A, B, C, |D|, and
).
The decomposed polarization matrices (20) are described by five
quantities (A, B, C, |D|, and ![]() ]), whose values can be obtained
from the covariance measurements and from the polarization constraint
BC
= |D|2. This gives
]), whose values can be obtained
from the covariance measurements and from the polarization constraint
BC
= |D|2. This gives
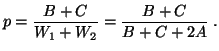
![]() ,
it can be shown that
,
it can be shown that
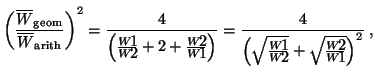
![]() and the means ratio are functions of the
particular basis in which the polarization measurements are made, but p is
independent of basis. In an H-V basis,
and the means ratio are functions of the
particular basis in which the polarization measurements are made, but p is
independent of basis. In an H-V basis,
![]() ,
and
,
and