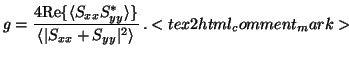 |
The depolarization produced by randomly oriented scatterers can be shown to
depend only on the sphericity parameter g (Scott, 1999; Krehbiel and
Scott, 1999), where
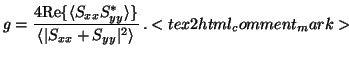 |
![$\displaystyle \frac{\langle \vert S_{xx}+ S_{yy}\vert^2 \rangle}{{\rm Re}\{\lan...
...rac{1}{f\cos\delta_\ell}\left [ \sqrt{ZDR} + \frac{1}{\sqrt{ZDR}} \right ]
\, ,$](img151.gif) |
Figure 11 shows how g varies with ZDR and
![]() .
The top
graph shows that g is a maximum when the particles are spherical (ZDR= 0 dB) and decreases as the particles depart from sphericity; hence the
term sphericity parameter for g. The bottom graph shows how g is related
to to
.
The top
graph shows that g is a maximum when the particles are spherical (ZDR= 0 dB) and decreases as the particles depart from sphericity; hence the
term sphericity parameter for g. The bottom graph shows how g is related
to to
![]() for different values of ZDR. For
for different values of ZDR. For
![]() positive,
0 < g< 1. g is unity only in the limiting case when ZDR and
positive,
0 < g< 1. g is unity only in the limiting case when ZDR and
![]() are unity. The dashed
are unity. The dashed ![]() line in the upper right quadrant of the
graph indicates when the two quantities are equal; g is greater or less
than
line in the upper right quadrant of the
graph indicates when the two quantities are equal; g is greater or less
than
![]() depending on ZDR and the particular value of
depending on ZDR and the particular value of
![]() .
.
 |
An interesting situation occurs if
![]() were to ever reverse sign.
The terms in the denominator of (34) would then tend to cancel and
g would become large and negative. It turns out that this would cause
the polarization state to suddenly switch from the top to the bottom half of
the Poincaré sphere (or vice versa) and be near the circular polarization pole
(Krehbiel and Scott, 1999). Such a sign reversal would occur if
were to ever reverse sign.
The terms in the denominator of (34) would then tend to cancel and
g would become large and negative. It turns out that this would cause
the polarization state to suddenly switch from the top to the bottom half of
the Poincaré sphere (or vice versa) and be near the circular polarization pole
(Krehbiel and Scott, 1999). Such a sign reversal would occur if
![]() .
Since
.
Since
![]() is the phase difference of backscattered Hand V signals if the aligned particles were aligned, such a situation
would arise only at higher order resonances in the Mie scattering regime
or when the particles are highly elongated. Such an effect, if it occurs in
nature, would provide a strong signature of randomly oriented particles.
is the phase difference of backscattered Hand V signals if the aligned particles were aligned, such a situation
would arise only at higher order resonances in the Mie scattering regime
or when the particles are highly elongated. Such an effect, if it occurs in
nature, would provide a strong signature of randomly oriented particles.